Publications
Journal Papers
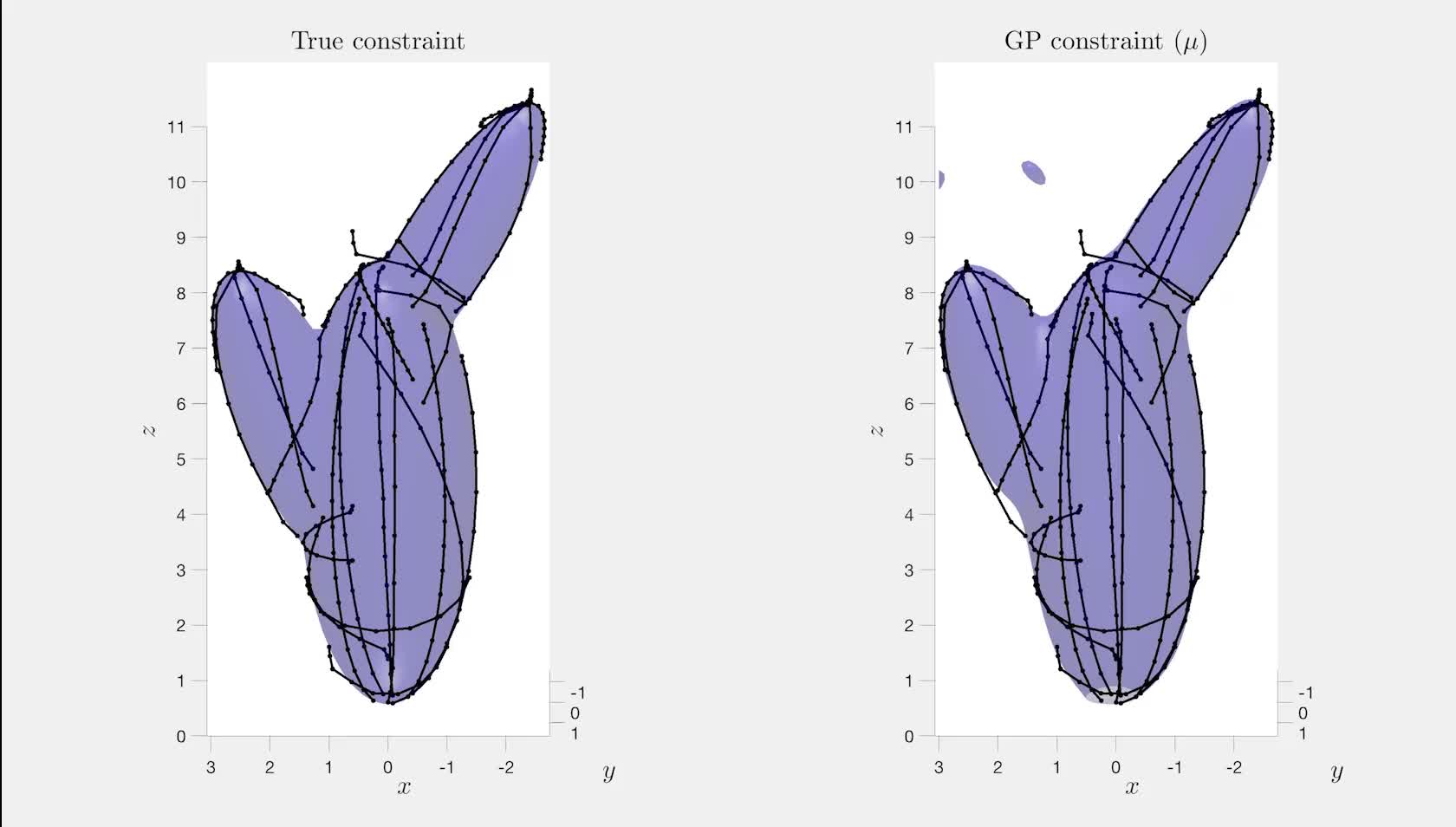 |
Gaussian Process Constraint Learning for Scalable Chance-Constrained Motion Planning From Demonstrations Glen Chou*, Hao Wang*, Dmitry Berenson IEEE Robotics and Automation Letters (RA-L), with presentation at ICRA 2022, vol. 7, no. 2, pp. 3827-3834, April 2022. [Abstract] [arXiv] [DOI] [Supplementary Video] [Cite] |
|
Abstract: We propose a method for learning constraints represented as Gaussian processes (GPs) from locally-optimal demonstrations. Our approach uses the Karush-Kuhn-Tucker (KKT) optimality conditions to determine where on the demonstrations the constraint is tight, and a scaling of the constraint gradient at those states. We then train a GP representation of the constraint which is consistent with and which generalizes this information. We further show that the GP uncertainty can be used within a kinodynamic RRT to plan probabilistically-safe trajectories, and that we can exploit the GP structure within the planner to exactly achieve a specified safety probability. We demonstrate our method can learn complex, nonlinear constraints demonstrated on a 5D nonholonomic car, a 12D quadrotor, and a 3-link planar arm, all while requiring minimal prior information on the constraint. Our results suggest the learned GP constraint is accurate, outperforming previous constraint learning methods that require more a priori knowledge. |
||
BibTeX:
@inproceedings{Chou-RAL-22, |
||
 |
Learning Temporal Logic Formulas from Suboptimal Demonstrations: Theory and Experiments Glen Chou, Necmiye Ozay, Dmitry Berenson Autonomous Robots (AURO), vol. 46, no. 1, pp. 149-174, January 2022. [Abstract] [DOI] [Supplementary Video] [Cite] |
|
Abstract: We present a method for learning multi-stage tasks from demonstrations by learning the logical structure and atomic propositions of a consistent linear temporal logic (LTL) formula. The learner is given successful but potentially suboptimal demonstrations, where the demonstrator is optimizing a cost function while satisfying the LTL formula, and the cost function is uncertain to the learner. Our algorithm uses the Karush-Kuhn-Tucker (KKT) optimality conditions of the demonstrations together with a counterexample-guided falsification strategy to learn the atomic proposition parameters and logical structure of the LTL formula, respectively. We provide theoretical guarantees on the conservativeness of the recovered atomic proposition sets, as well as completeness in the search for finding an LTL formula consistent with the demonstrations. We evaluate our method on high-dimensional nonlinear systems by learning LTL formulas explaining multi-stage tasks on a simulated 7-DOF arm and a quadrotor, and show that it outperforms competing methods for learning LTL formulas from positive examples. Finally, we demonstrate that our approach can learn a real-world multi-stage tabletop manipulation task on a physical 7-DOF Kuka iiwa arm. |
||
BibTeX:
@inproceedings{Chou-AURO-21, |
||
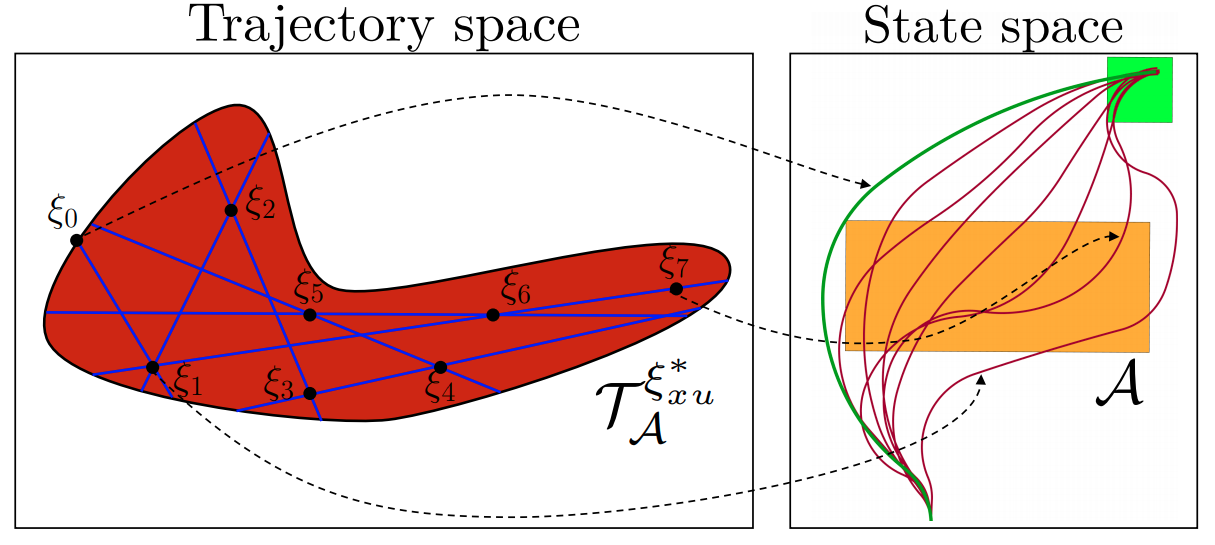 |
Learning Constraints from Demonstrations with Grid and Parametric Representations Glen Chou, Dmitry Berenson, Necmiye Ozay International Journal of Robotics Research (IJRR), vol. 40, no. 10-11, pp. 1255-1283, September 2021. [Abstract] [DOI] [Cite] |
|
Abstract: We extend the learning from demonstration paradigm by providing a method for learning unknown constraints shared across tasks, using demonstrations of the tasks, their cost functions, and knowledge of the system dynamics and control constraints. Given safe demonstrations, our method uses hit-and-run sampling to obtain lower cost, and thus unsafe, trajectories. Both safe and unsafe trajectories are used to obtain a consistent representation of the unsafe set via solving an integer program. Our method generalizes across system dynamics and learns a guaranteed subset of the constraint. Additionally, by leveraging a known parameterization of the constraint, we modify our method to learn parametric constraints in high dimensions. We also provide theoretical analysis on what subset of the constraint and safe set can be learnable from safe demonstrations. We demonstrate our method on linear and nonlinear system dynamics, show that it can be modified to work with suboptimal demonstrations, and that it can also be used to learn constraints in a feature space. |
||
BibTeX:
@inproceedings{Chou-IJRR-21, |
||
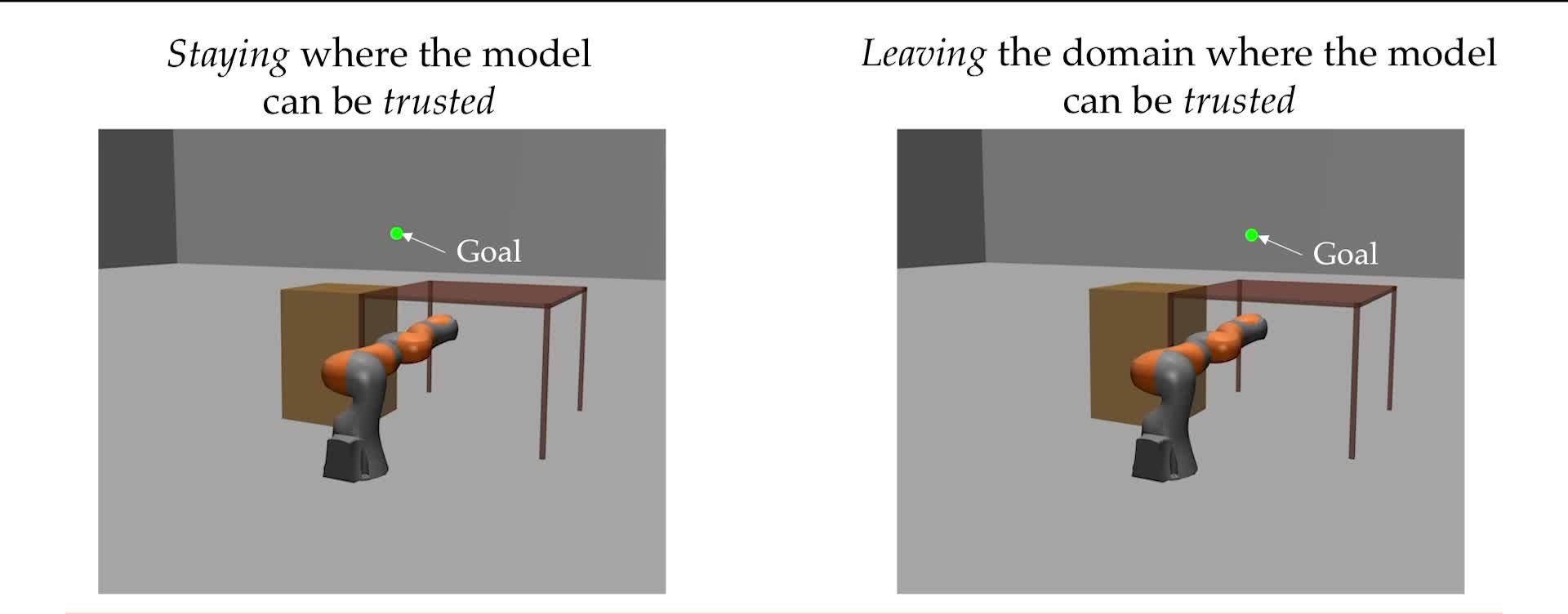 |
Planning with Learned Dynamics: Probabilistic Guarantees on Safety and Reachability via Lipschitz Constants Craig Knuth*, Glen Chou*, Necmiye Ozay, Dmitry Berenson IEEE Robotics and Automation Letters (RA-L), with presentation at ICRA 2021, vol. 6, no. 3, pp. 5129-5136, July 2021. [Abstract] [arXiv] [DOI] [Supplementary Video] [Cite] |
|
Abstract: We present a method for feedback motion planning of systems with unknown dynamics which provides probabilistic guarantees on safety, reachability, and goal stability. To find a domain in which a learned control-affine approximation of the true dynamics can be trusted, we estimate the Lipschitz constant of the difference between the true and learned dynamics, and ensure the estimate is valid with a given probability. Provided the system has at least as many controls as states, we also derive existence conditions for a one-step feedback law which can keep the real system within a small bound of a nominal trajectory planned with the learned dynamics. Our method imposes the feedback law existence as a constraint in a sampling-based planner, which returns a feedback policy around a nominal plan ensuring that, if the Lipschitz constant estimate is valid, the true system is safe during plan execution, reaches the goal, and is ultimately invariant in a small set about the goal. We demonstrate our approach by planning using learned models of a 6D quadrotor and a 7DOF Kuka arm. We show that a baseline which plans using the same learned dynamics without considering the error bound or the existence of the feedback law can fail to stabilize around the plan and become unsafe. |
||
BibTeX:
@inproceedings{Knuth-RAL-21, |
||
 |
Learning Constraints from Locally-Optimal Demonstrations under Cost Function Uncertainty Glen Chou, Necmiye Ozay, Dmitry Berenson IEEE Robotics and Automation Letters (RA-L), with presentation at ICRA 2020, vol. 5, no. 2, pp. 3682-3690, April 2020. [Abstract] [arXiv] [DOI] [Supplementary Video] [Cite] |
|
Abstract: We present an algorithm for learning parametric constraints from locally-optimal demonstrations, where the cost function being optimized is uncertain to the learner. Our method uses the Karush-Kuhn-Tucker (KKT) optimality conditions of the demonstrations within a mixed integer linear program (MILP) to learn constraints which are consistent with the local optimality of the demonstrations, by either using a known constraint parameterization or by incrementally growing a parameterization that is consistent with the demonstrations. We provide theoretical guarantees on the conservativeness of the recovered safe/unsafe sets and analyze the limits of constraint learnability when using locally-optimal demonstrations. We evaluate our method on high-dimensional constraints and systems by learning constraints for 7-DOF arm and quadrotor examples, show that it outperforms competing constraint-learning approaches, and can be effectively used to plan new constraint-satisfying trajectories in the environment. |
||
BibTeX:
@inproceedings{Chou-RAL-20, |
||
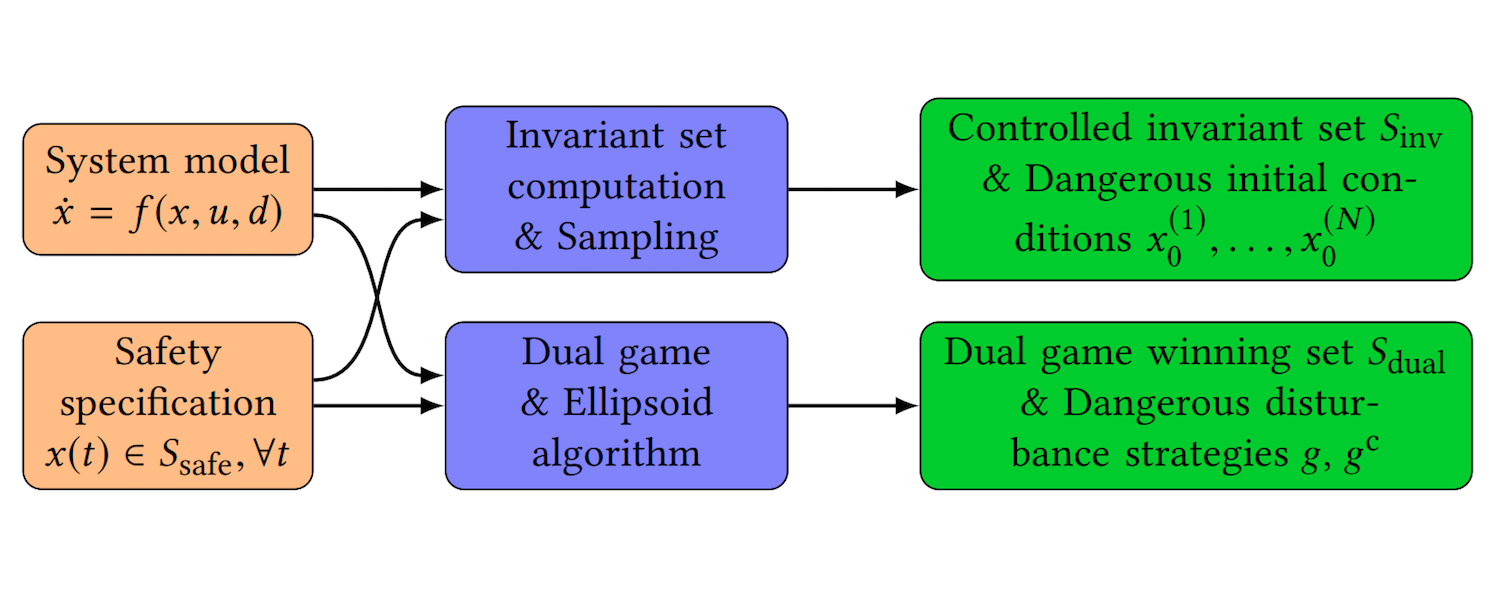 |
Using control synthesis to generate corner cases: A case study on autonomous driving Glen Chou*, Yunus E. Sahin*, Liren Yang*, Kwesi J. Rutledge, Petter Nilsson, Necmiye Ozay IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems (ESWEEK-TCAD special issue), vol. 37, no. 11, pp. 2906-2917, November 2018. [Abstract] [arXiv] [DOI] [Cite] Also presented at 2018 University of Michigan Engineering Graduate Symposium; won Emerging Research Social Impact award. |
|
Abstract: This paper employs correct-by-construction control synthesis, in particular controlled invariant set computations, for falsification. Our hypothesis is that if it is possible to compute a “large enough" controlled invariant set either for the actual system model or some simplification of the system model, interesting corner cases for other control designs can be generated by sampling initial conditions from the boundary of this controlled invariant set. Moreover, if falsifying trajectories for a given control design can be found through such sampling, then the controlled invariant set can be used as a supervisor to ensure safe operation of the control design under consideration. In addition to interesting initial conditions, which are mostly related to safety violations in transients, we use solutions from a dual game, a reachability game for the safety specification, to find falsifying inputs. We also propose optimization-based heuristics for input generation for cases when the state is outside the winning set of the dual game. To demonstrate the proposed ideas, we consider case studies from basic autonomous driving functionality, in particular, adaptive cruise control and lane keeping. We show how the proposed technique can be used to find interesting falsifying trajectories for classical control designs like proportional controllers, proportional integral controllers and model predictive controllers, as well as an open source real-world autonomous driving package. |
||
BibTeX:
@article{Chou-et-al-Journal-18, |
||
Notes: Also presented at 2018 University of Michigan Engineering Graduate Symposium; won Emerging Research Social Impact award. |
||
Peer-Reviewed Conference Papers
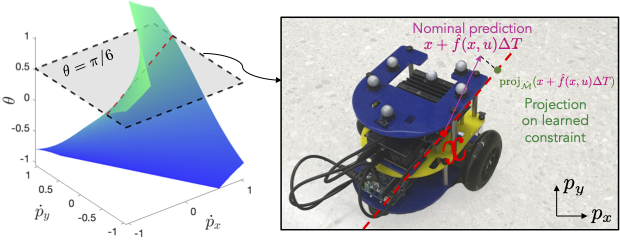 |
Improving Out-of-Distribution Generalization of Learned Dynamics by Learning Pseudometrics and Constraint Manifolds Yating Lin, Glen Chou, Dmitry Berenson Proceedings of the 61st IEEE International Conference on Robotics and Automation (ICRA), May 2024. [Abstract] [arXiv] [PDF] [Cite] |
||
Abstract: We propose a method for improving the prediction accuracy of learned robot dynamics models on out-of-distribution (OOD) states. We achieve this by leveraging two key sources of structure often present in robot dynamics: 1) sparsity, i.e., some components of the state may not affect the dynamics, and 2) physical limits on the set of possible motions, in the form of nonholonomic constraints. Crucially, we do not assume this structure is known a priori, and instead learn it from data. We use contrastive learning to obtain a distance pseudometric that uncovers the sparsity pattern in the dynamics, and use it to reduce the input space when learning the dynamics. We then learn the unknown constraint manifold by approximating the normal space of possible motions from the data, which we use to train a Gaussian process (GP) representation of the constraint manifold. We evaluate our approach on a physical differential-drive robot and a simulated quadrotor, showing improved prediction accuracy on OOD data relative to baselines. |
|||
BibTeX:
@inproceedings{Lin-ICRA-24, |
|||
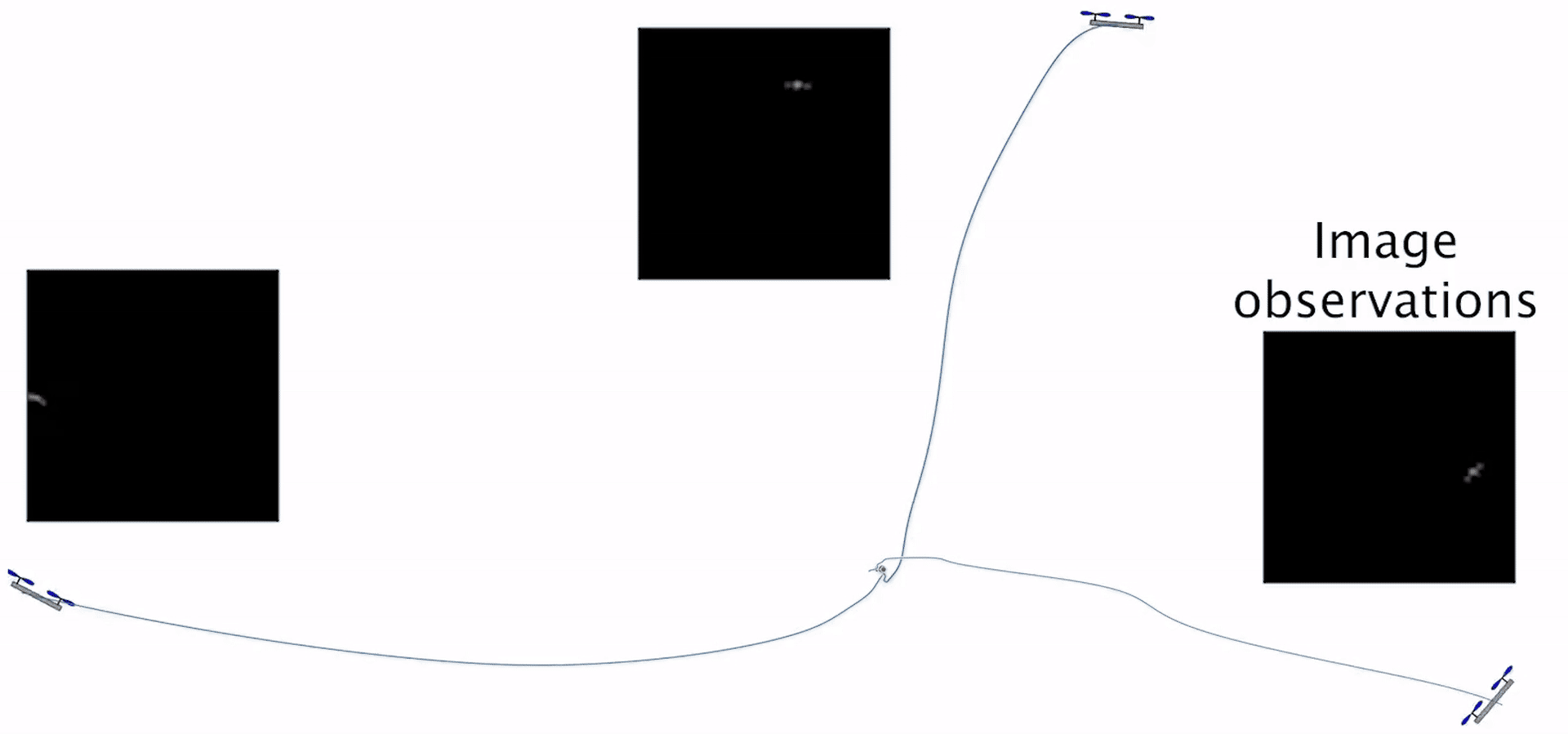 |
Synthesizing Stable Reduced-Order Visuomotor Policies for Nonlinear Systems via Sums-of-Squares Optimization Glen Chou, Russ Tedrake Proceedings of the 62nd IEEE Conference on Decision and Control (CDC), December 2023. [Abstract] [arXiv] [PDF] [Cite] |
||
Abstract: We present a method for synthesizing dynamic, reduced-order output-feedback polynomial control policies for control-affine nonlinear systems which guarantees runtime stability to a goal state, when using visual observations and a learned perception module in the feedback control loop. We leverage Lyapunov analysis to formulate the problem of synthesizing such policies. This problem is nonconvex in the policy parameters and the Lyapunov function that is used to prove the stability of the policy. To solve this problem approximately, we propose two approaches: the first solves a sequence of sum-of-squares optimization problems to iteratively improve a policy which is provably-stable by construction, while the second directly performs gradient-based optimization on the parameters of the polynomial policy, and its closed-loop stability is verified a posteriori. We extend our approach to provide stability guarantees in the presence of observation noise, which realistically arises due to errors in the learned perception module. We evaluate our approach on several underactuated nonlinear systems, including pendula and quadrotors, showing that our guarantees translate to empirical stability when controlling these systems from images, while baseline approaches can fail to reliably stabilize the system. |
|||
BibTeX:
@inproceedings{Chou-CDC-23, |
|||
 |
Fighting Uncertainty with Gradients: Offline Reinforcement Learning via Diffusion Score Matching H.J. Terry Suh, Glen Chou*, Hongkai Dai*, Lujie Yang*, Abhishek Gupta, Russ Tedrake 7th Conference on Robot Learning (CoRL), November 2023. [Abstract] [arXiv] [PDF] [Supplementary Video] [Code] [Website] [Cite] |
||
Abstract: Offline optimization paradigms such as offline Reinforcement Learning (RL) or Imitation Learning (IL) allow policy search algorithms to make use of offline data, but require careful incorporation of uncertainty in order to circumvent the challenges of distribution shift. Gradient-based policy search methods are a promising direction due to their effectiveness in high dimensions; however, we require a more careful consideration of how these methods interplay with uncertainty estimation. We claim that in order for an uncertainty metric to be amenable for gradient-based optimization, it must be (i) stably convergent to data when uncertainty is minimized with gradients, and (ii) not prone to underestimation of true uncertainty. We investigate smoothed distance to data as a metric, and show that it not only stably converges to data, but also allows us to analyze model bias with Lipschitz constants. Moreover, we establish an equivalence between smoothed distance to data and data likelihood, which allows us to use score-matching techniques to learn gradients of distance to data. Importantly, we show that offline model-based policy search problems that maximize data likelihood do not require values of likelihood; but rather only the gradient of the log likelihood (the score function). Using this insight, we propose Score-Guided Planning (SGP), a planning algorithm for offline RL that utilizes score-matching to enable first-order planning in high-dimensional problems, where zeroth-order methods were unable to scale, and ensembles were unable to overcome local minima. |
|||
BibTeX:
@inproceedings{Suh-CoRL-23, |
|||
 |
Statistical Safety and Robustness Guarantees for Feedback Motion Planning of Unknown Underactuated Stochastic Systems Craig Knuth, Glen Chou, Jamie Reese, Joseph Moore Proceedings of the 60th IEEE International Conference on Robotics and Automation (ICRA), May 2023. [Abstract] [arXiv] [PDF] [Cite] |
||
Abstract: We present a method for providing statistical guarantees on runtime safety and goal reachability for integrated planning and control of a class of systems with unknown nonlinear stochastic underactuated dynamics. Specifically, given a dynamics dataset, our method jointly learns a mean dynamics model, a spatially-varying disturbance bound that captures the effect of noise and model mismatch, and a feedback controller based on contraction theory that stabilizes the learned dynamics. We propose a sampling-based planner that uses the mean dynamics model and simultaneously bounds the closed-loop tracking error via a learned disturbance bound. We employ techniques from Extreme Value Theory (EVT) to estimate, to a specified level of confidence, several constants which characterize the learned components and govern the size of the tracking error bound. This ensures plans are guaranteed to be safely tracked at runtime. We validate that our guarantees translate to empirical safety in simulation on a 10D quadrotor, and in the real world on a physical CrazyFlie quadrotor and Clearpath Jackal robot, whereas baselines that ignore the model error and stochasticity are unsafe. |
|||
BibTeX:
@inproceedings{Knuth-ICRA-23, |
|||
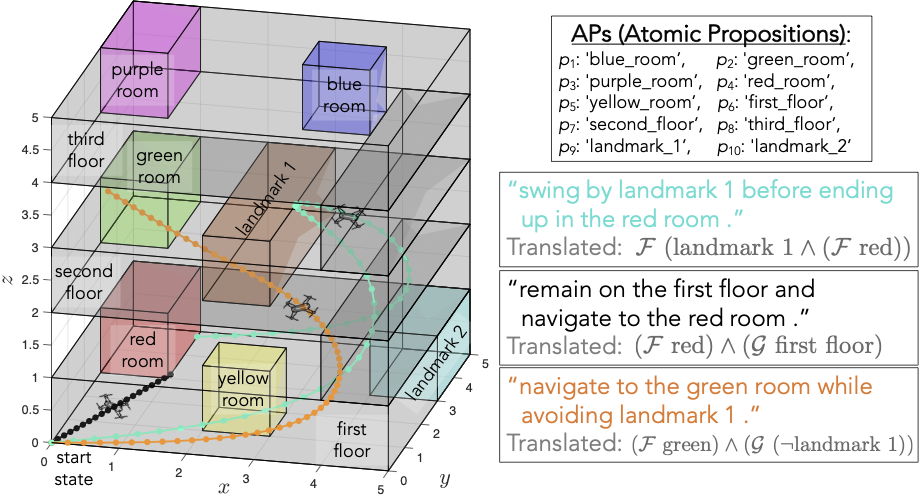 |
Data-Efficient Learning of Natural Language to Linear Temporal Logic Translators for Robot Task Specification Jiayi Pan, Glen Chou, Dmitry Berenson Proceedings of the 60th IEEE International Conference on Robotics and Automation (ICRA), May 2023. [Abstract] [arXiv] [PDF] [Supplementary Video] [Code] [Cite] |
||
Abstract: To make robots accessible to a broad audience, it is critical to endow them with the ability to take universal modes of communication, like commands given in natural language, and extract a concrete desired task specification, defined using a formal language like linear temporal logic (LTL). In this paper, we present a learning-based approach for translating from natural language commands to LTL specifications with very limited human-labeled training data. This is in stark contrast to existing natural-language to LTL translators, which require large human-labeled datasets, often in the form of labeled pairs of LTL formulas and natural language commands, to train the translator. To reduce reliance on human data, our approach generates a large synthetic training dataset through algorithmic generation of LTL formulas, conversion to structured English, and then exploiting the paraphrasing capabilities of modern large language models (LLMs) to synthesize a diverse corpus of natural language commands corresponding to the LTL formulas. We use this generated data to finetune an LLM and apply a constrained decoding procedure at inference time to ensure the returned LTL formula is syntactically correct. We evaluate our approach on three existing LTL/natural language datasets and show that we can translate natural language commands at 75% accuracy with far less human data (≤12 annotations). Moreover, when training on large human-annotated datasets, our method achieves higher test accuracy (95% on average) than prior work. Finally, we show the translated formulas can be used to plan long-horizon, multi-stage tasks on a 12D quadrotor. |
|||
BibTeX:
@inproceedings{Pan-ICRA-23, |
|||
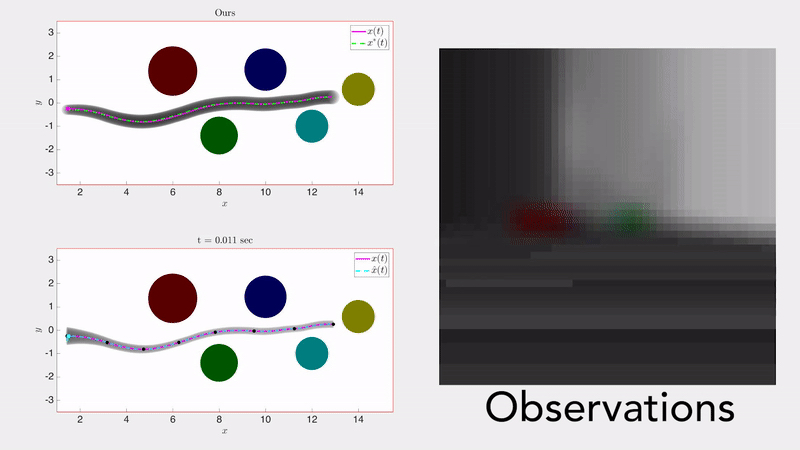 |
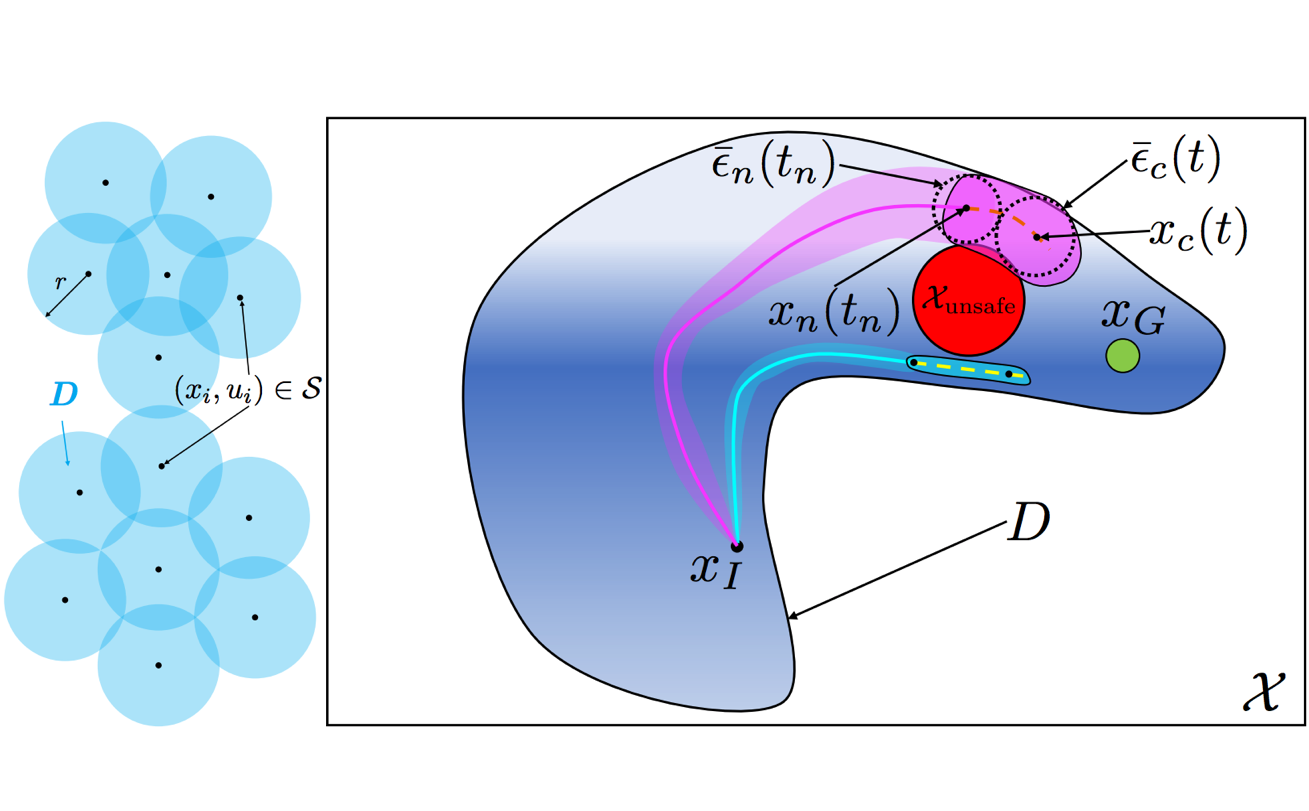
Safe Output Feedback Motion Planning from Images via Learned Perception Modules and Contraction Theory Glen Chou, Necmiye Ozay, Dmitry Berenson Proceedings of the 15th International Workshop on the Algorithmic Foundations of Robotics (WAFR), June 2022. [Abstract] [arXiv] [DOI] [Talk] [Cite] |
||
Abstract: We present a motion planning algorithm for a class of uncertain control-affine nonlinear systems which guarantees runtime safety and goal reachability when using high-dimensional sensor measurements (e.g., RGB-D images) and a learned perception module in the feedback control loop. First, given a dataset of states and observations, we train a perception system that seeks to invert a subset of the state from an observation, and estimate an upper bound on the perception error which is valid with high probability in a trusted domain near the data. Next, we use contraction theory to design a stabilizing state feedback controller and a convergent dynamic state observer which uses the learned perception system to update its state estimate. We derive a bound on the trajectory tracking error when this controller is subjected to errors in the dynamics and incorrect state estimates. Finally, we integrate this bound into a sampling-based motion planner, guiding it to return trajectories that can be safely tracked at runtime using sensor data. We demonstrate our approach in simulation on a 4D car, a 6D planar quadrotor, and a 17D manipulation task with RGB(-D) sensor measurements, demonstrating that our method safely and reliably steers the system to the goal, while baselines that fail to consider the trusted domain or state estimation errors can be unsafe. |
|||
BibTeX:
@inproceedings{Chou-WAFR-22, |
|||
 |
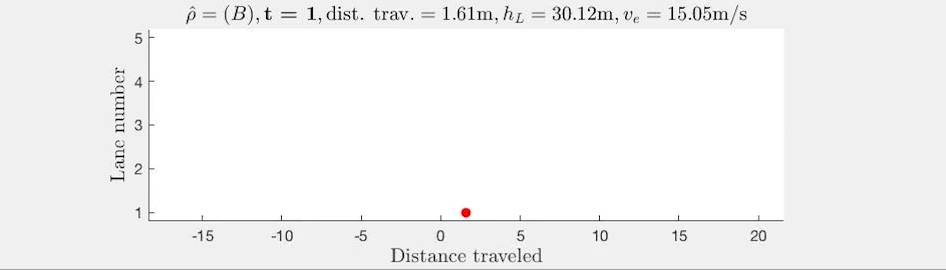
Model Error Propagation via Learned Contraction Metrics for Safe Feedback Motion Planning of Unknown Systems Glen Chou, Necmiye Ozay, Dmitry Berenson Proceedings of the 60th IEEE Conference on Decision and Control (CDC), December 2021. [Abstract] [arXiv] [DOI] [Supplementary Video] [Cite] |
||
Abstract: We present a method for contraction-based feedback motion planning of locally incrementally exponentially stabilizable systems with unknown dynamics that provides probabilistic safety and reachability guarantees. Given a dynamics dataset, our method learns a deep control-affine approximation of the dynamics. To find a trusted domain where this model can be used for planning, we obtain an estimate of the Lipschitz constant of the model error, which is valid with a given probability, in a region around the training data, providing a local, spatially-varying model error bound. We derive a trajectory tracking error bound for a contraction-based controller that is subjected to this model error, and then learn a controller that optimizes this tracking bound. With a given probability, we verify the correctness of the controller and tracking error bound in the trusted domain. We then use the trajectory error bound together with the trusted domain to guide a sampling-based planner to return trajectories that can be robustly tracked in execution. We show results on a 4D car, a 6D quadrotor, and a 22D deformable object manipulation task, showing our method plans safely with learned models of high-dimensional underactuated systems, while baselines that plan without considering the tracking error bound or the trusted domain can fail to stabilize the system and become unsafe. |
|||
BibTeX:
@inproceedings{Chou-CDC-21, |
|||
 |
Compositional Safety Rules for Inter-Triggering Hybrid Automata Kwesi J. Rutledge*, Glen Chou*, Necmiye Ozay Proceedings of the 24th International Conference on Hybrid Systems: Computation and Control (HSCC), May 2021. [Abstract] [PDF] [DOI] [Supplementary Video] [Cite] |
||
Abstract: In this paper, we present a compositional condition for ensuring safety of a collection of interacting systems modeled by inter-triggering hybrid automata (ITHA). ITHA is a modeling formalism for representing multi-agent systems in which each agent is governed by individual dynamics but can also interact with other agents through triggering actions. These triggering actions result in a jump/reset in the state of other agents according to a global resolution function. A sufficient condition for safety of the collection, inspired by responsibility-sensitive safety, is developed in two parts: self-safety relating to the individual dynamics, and responsibility relating to the triggering actions. The condition relies on having an over-approximation method for the resolution function. We further show how such over-approximations can be obtained and improved via communication. We use two examples, a job scheduling task on parallel processors and a highway driving example, throughout the paper to illustrate the concepts. Finally, we provide a comprehensive evaluation on how the proposed condition can be leveraged for several multi-agent control and supervision examples. |
|||
BibTeX:
@inproceedings{Rutledge-HSCC-21, |
|||
 |
Uncertainty-Aware Constraint Learning for Adaptive Safe Motion Planning from Demonstrations Glen Chou, Necmiye Ozay, Dmitry Berenson Proceedings of the 4th Conference on Robot Learning (CoRL), November 2020. [Abstract] [arXiv] [PDF] [Talk] [Supplementary Video] [Cite] |
||
Abstract: We present a method for learning to satisfy uncertain constraints from demonstrations. Our method uses robust optimization to obtain a belief over the potentially infinite set of possible constraints consistent with the demonstrations, and then uses this belief to plan trajectories that trade off performance with satisfying the possible constraints. We use these trajectories in a closed-loop policy that executes and replans using belief updates, which incorporate data gathered during execution. We derive guarantees on the accuracy of our constraint belief and probabilistic guarantees on plan safety. We present results on a 7-DOF arm and 12D quadrotor, showing our method can learn to satisfy high-dimensional (up to 30D) uncertain constraints, and outperforms baselines in safety and efficiency. |
|||
BibTeX:
@inproceedings{Chou-CoRL-20, |
|||
 |
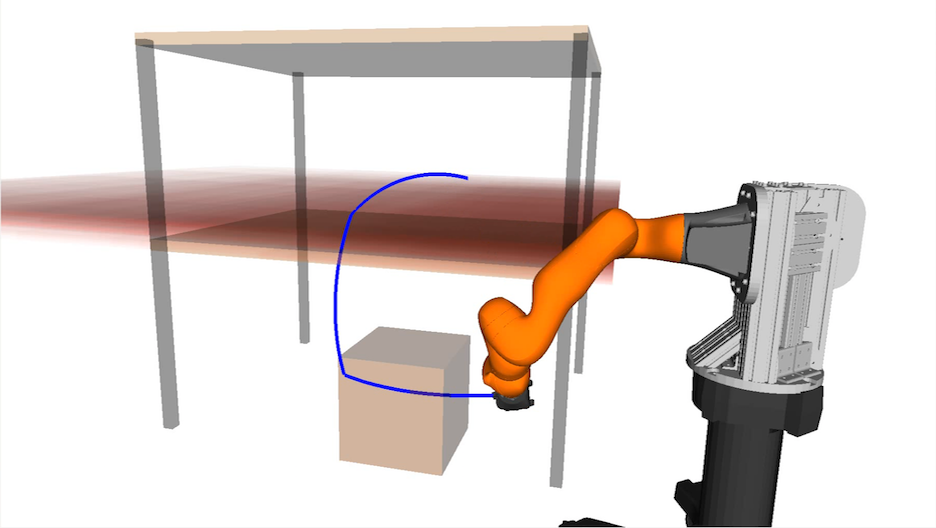
Explaining Multi-stage Tasks by Learning Temporal Logic Formulas from Suboptimal Demonstrations Glen Chou, Necmiye Ozay, Dmitry Berenson Proceedings of Robotics: Science and Systems (RSS) XVI, July 2020. [Abstract] [arXiv] [DOI] [Talk] [Supplementary Video] [Cite] Invited to AURO special issue. |
||
Abstract: We present a method for learning multi-stage tasks from demonstrations by learning the logical structure and atomic propositions of a consistent linear temporal logic (LTL) formula. The learner is given successful but potentially suboptimal demonstrations, where the demonstrator is optimizing a cost function while satisfying the LTL formula, and the cost function is uncertain to the learner. Our algorithm uses the Karush-Kuhn-Tucker (KKT) optimality conditions of the demonstrations together with a counterexample-guided falsification strategy to learn the atomic proposition parameters and logical structure of the LTL formula, respectively. We provide theoretical guarantees on the conservativeness of the recovered atomic proposition sets, as well as completeness in the search for finding an LTL formula consistent with the demonstrations. We evaluate our method on high-dimensional nonlinear systems by learning LTL formulas explaining multi-stage tasks on 7-DOF arm and quadrotor systems and show that it outperforms competing methods for learning LTL formulas from positive examples. |
|||
BibTeX:
@inproceedings{Chou-RSS-20, |
|||
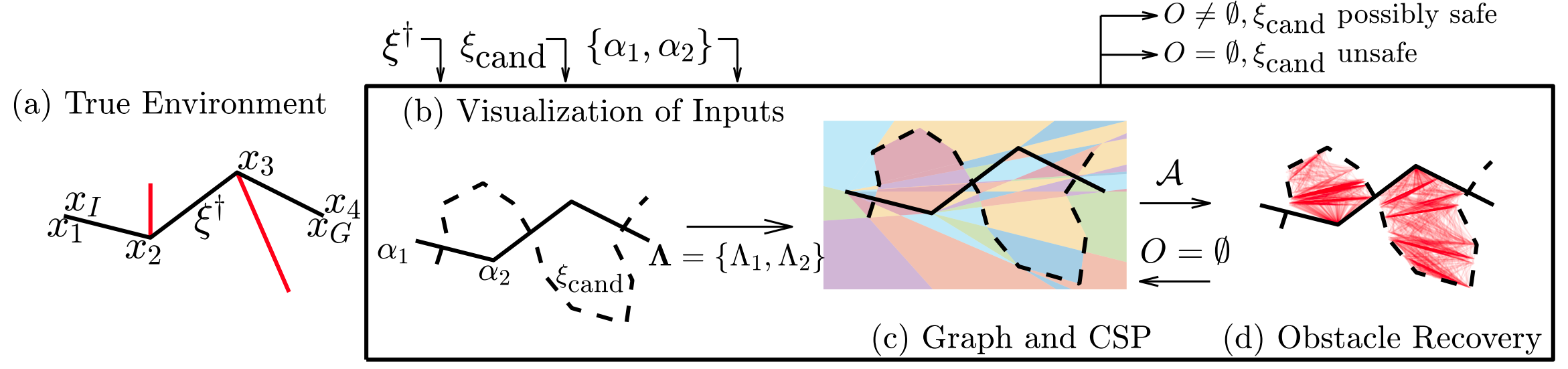 |
Inferring Obstacles and Path Validity from Visibility-Constrained Demonstrations Craig Knuth, Glen Chou, Necmiye Ozay, Dmitry Berenson Proceedings of the 14th International Workshop on the Algorithmic Foundations of Robotics (WAFR), June 2020. [Abstract] [arXiv] [DOI] [Cite] |
||
Abstract: Many methods in learning from demonstration assume that the demonstrator has knowledge of the full environment. However, in many scenarios, a demonstrator only sees part of the environment and they continuously replan as they gather information. To plan new paths or to reconstruct the environment, we must consider the visibility constraints and replanning process of the demonstrator, which, to our knowledge, has not been done in previous work. We consider the problem of inferring obstacle configurations in a 2D environment from demonstrated paths for a point robot that is capable of seeing in any direction but not through obstacles. Given a set of \textit{survey points}, which describe where the demonstrator obtains new information, and a candidate path, we construct a Constraint Satisfaction Problem (CSP) on a cell decomposition of the environment. We parameterize a set of obstacles corresponding to an assignment from the CSP and sample from the set to find valid environments. We show that there is a probabilistically-complete, yet not entirely tractable, algorithm that can guarantee novel paths in the space are unsafe or possibly safe. We also present an incomplete, but empirically-successful, heuristic-guided algorithm that we apply in our experiments to 1) planning novel paths and 2) recovering a probabilistic representation of the environment. |
|||
BibTeX:
@inproceedings{Knuth-WAFR-20, |
|||
 |
Learning Parametric Constraints in High Dimensions from Demonstrations Glen Chou, Necmiye Ozay, Dmitry Berenson Proceedings of the 3rd Conference on Robot Learning (CoRL), November 2019. [Abstract] [arXiv] [PDF] [Cite] |
||
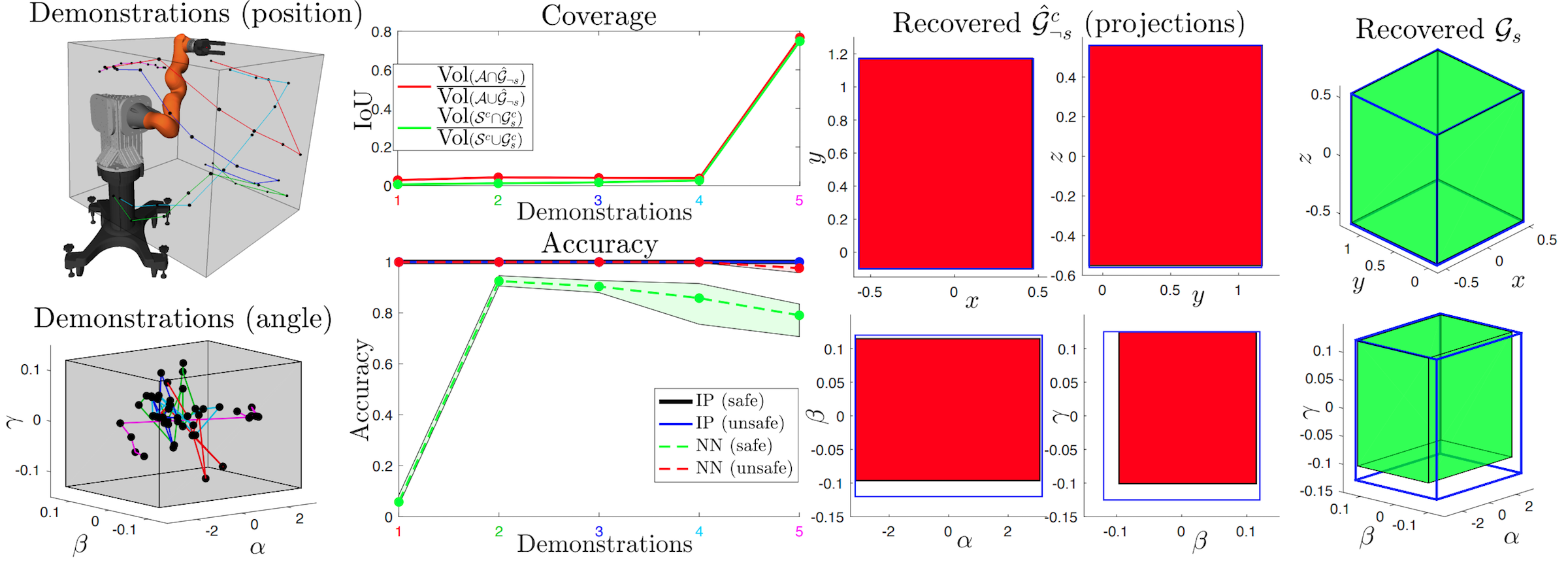
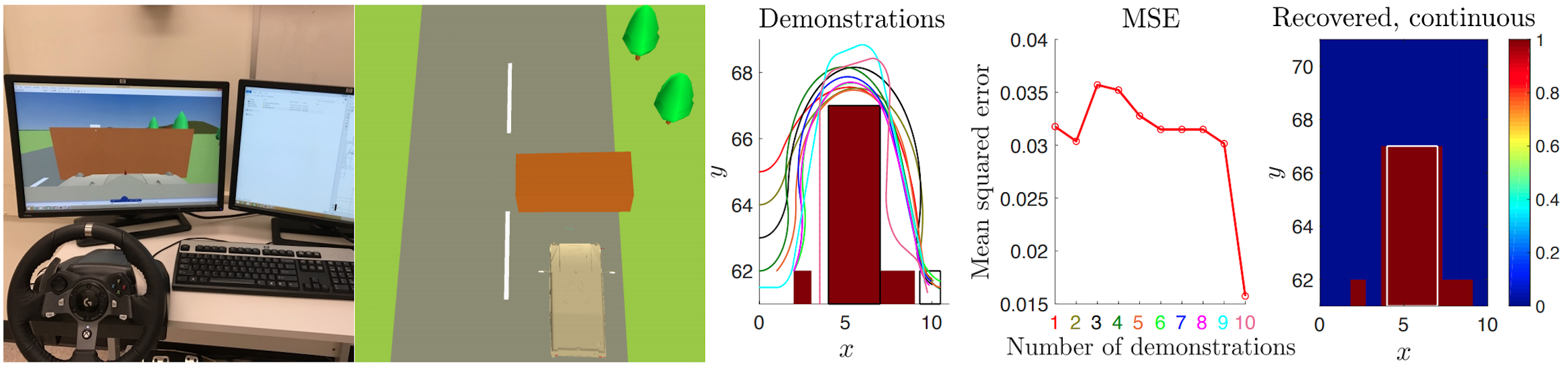
Abstract: We present a scalable algorithm for learning parametric constraints in high dimensions from safe expert demonstrations. To reduce the ill-posedness of the constraint recovery problem, our method uses hit-and-run sampling to generate lower cost, and thus unsafe, trajectories. Both safe and unsafe trajectories are used to obtain a representation of the unsafe set that is compatible with the data by solving an integer program in that representation's parameter space. Our method can either leverage a known parameterization or incrementally grow a parameterization while remaining consistent with the data, and we provide theoretical guarantees on the conservativeness of the recovered unsafe set. We evaluate our method on high-dimensional constraints for high-dimensional systems by learning constraints for 7-DOF arm, quadrotor, and planar pushing examples, and show that our method outperforms baseline approaches. |
|||
BibTeX:
@inproceedings{Chou-CoRL-19, |
|||
 |
Learning Constraints from Demonstrations Glen Chou, Dmitry Berenson, Necmiye Ozay Proceedings of the 14th International Workshop on the Algorithmic Foundations of Robotics (WAFR), December 2018. [Abstract] [arXiv] [DOI] [Cite] Invited to IJRR special issue. |
||
Abstract: We extend the learning from demonstration paradigm by providing a method for learning unknown constraints shared across tasks, using demonstrations of the tasks, their cost functions, and knowledge of the system dynamics and control constraints. Given safe demonstrations, our method uses hit-and-run sampling to obtain lower cost, and thus unsafe, trajectories. Both safe and unsafe trajectories are used to obtain a consistent representation of the unsafe set via solving an integer program. Our method generalizes across system dynamics and learns a guaranteed subset of the constraint. We also provide theoretical analysis on what subset of the constraint can be learnable from safe demonstrations. We demonstrate our method on linear and nonlinear system dynamics, show that it can be modi ed to work with suboptimal demonstrations, and that it can also be used to solve a transfer learning task. |
|||
BibTeX:
@inproceedings{Chou-WAFR-18, |
|||
 |
Using control synthesis to generate corner cases: A case study on autonomous driving Glen Chou*, Yunus E. Sahin*, Liren Yang*, Kwesi J. Rutledge, Petter Nilsson, Necmiye Ozay Proceedings of the ACM SIGBED International Conference on Embedded Software (EMSOFT), October 2018. [Abstract] [arXiv] [DOI] [Cite] Also presented at 2018 University of Michigan Engineering Graduate Symposium; won Emerging Research Social Impact award. |
||
Abstract: This paper employs correct-by-construction control synthesis, in particular controlled invariant set computations, for falsification. Our hypothesis is that if it is possible to compute a “large enough" controlled invariant set either for the actual system model or some simplification of the system model, interesting corner cases for other control designs can be generated by sampling initial conditions from the boundary of this controlled invariant set. Moreover, if falsifying trajectories for a given control design can be found through such sampling, then the controlled invariant set can be used as a supervisor to ensure safe operation of the control design under consideration. In addition to interesting initial conditions, which are mostly related to safety violations in transients, we use solutions from a dual game, a reachability game for the safety specification, to find falsifying inputs. We also propose optimization-based heuristics for input generation for cases when the state is outside the winning set of the dual game. To demonstrate the proposed ideas, we consider case studies from basic autonomous driving functionality, in particular, adaptive cruise control and lane keeping. We show how the proposed technique can be used to find interesting falsifying trajectories for classical control designs like proportional controllers, proportional integral controllers and model predictive controllers, as well as an open source real-world autonomous driving package. |
|||
BibTeX:
@inproceedings{Chou-et-al-EMSOFT-18, |
|||
 |
Incremental Segmentation of ARX Models Glen Chou, Necmiye Ozay, Dmitry Berenson Proceedings of the 18th IFAC Symposium on System Identification (SYSID), July 2018. [Abstract] [PDF] [DOI] [Cite] |
||
Abstract: We consider the problem of incrementally segmenting auto-regressive models with exogenous inputs (ARX models) when the data is received sequentially at run-time. In particular, we extend a recently proposed dynamic programming based polynomial-time algorithm for offline (batch) ARX model segmentation to the incremental setting. The new algorithm enables sequential updating of the models, eliminating repeated computation, while remaining optimal. We also show how certain noise bounds can be used to detect switches automatically at run-time. The efficiency of the approach compared to the batch method is illustrated on synthetic and real data. |
|||
BibTeX:
@inproceedings{Chou-SYSID-18, |
|||
 |
A Hybrid Framework for Multi-Vehicle Collision Avoidance Aparna Dhinakaran*, Mo Chen*, Glen Chou, Jennifer C. Shih, Claire J. Tomlin Proceedings of the 56th IEEE Conference on Decision and Control (CDC), December 2017. [Abstract] [arXiv] [DOI] [Cite] |
||
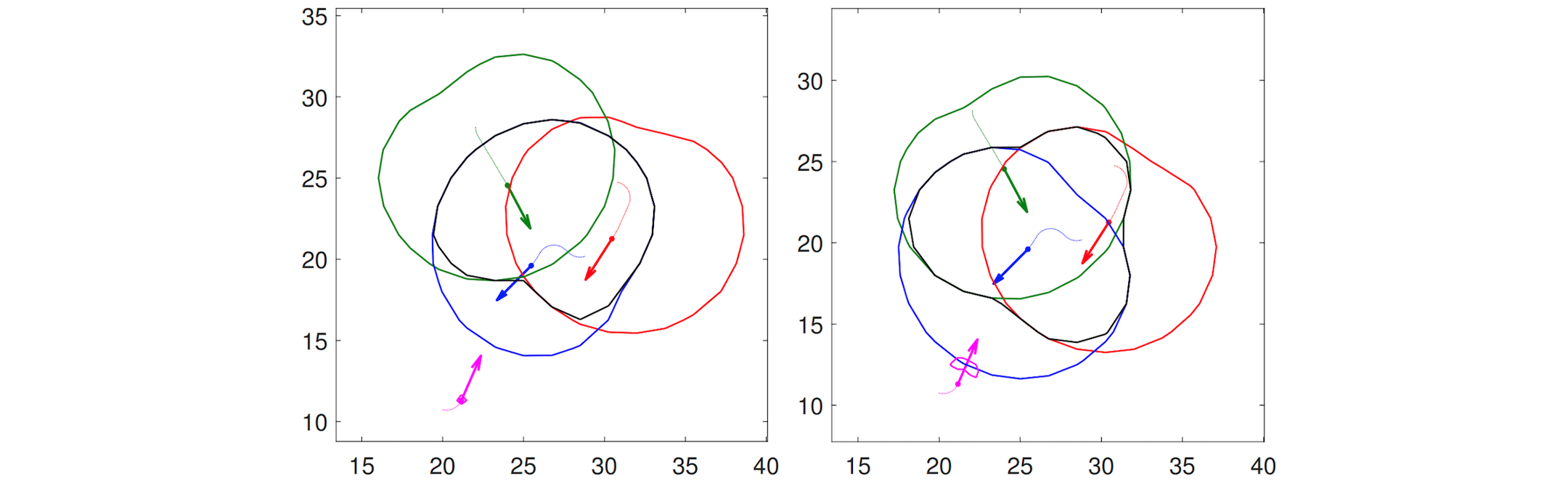
Abstract: With the recent surge of interest in UAVs for civilian services, the importance of developing tractable multi-agent analysis techniques that provide safety and performance guarantees have drastically increased. Hamilton-Jacobi (HJ) reachability has successfully provided these guarantees to small-scale systems and is flexible in terms of system dynamics. However, the exponential complexity scaling of HJ reachability with respect to system dimension prevents its direct application to larger-scale problems where the number of vehicles is greater than two. In this paper, we propose a collision avoidance algorithm using a hybrid framework for N+1 vehicles through higher-level control logic given any N-vehicle collision avoidance algorithm. Our algorithm conservatively approximates a guaranteed-safe region in the joint state space of the N+1 vehicles and produces a safety-preserving controller. In addition, our algorithm does not incur significant additional computation cost. We demonstrate our proposed method in simulation. |
|||
BibTeX:
@inproceedings{Dhinakaran-et-al-CDC-17,
author = {Aparna Dhinakaran and
Mo Chen and
Glen Chou and
Jennifer C. Shih and
Claire J. Tomlin},
title = {A hybrid framework for multi-vehicle collision avoidance},
booktitle = {56th {IEEE} Annual Conference on Decision and Control, {CDC} 2017,
Melbourne, Australia, December 12-15, 2017},
pages = {2979--2984},
year = {2017}, |
|||
Refereed Workshop Papers/Technical Reports
 |
Safely Integrating Perception, Planning, and Control for Robust Learning-Based Robot Autonomy Glen Chou* Robotics: Science and Systems, Pioneers Workshop, June 2022. [PDF] [Cite] |
||
BibTeX:
@inproceedings{Chou-RSSPioneersWS-22, |
|||
 |
Gaussian Process Constraint Learning for Scalable Safe Motion Planning from Demonstrations Hao Wang*, Glen Chou*, Dmitry Berenson Robotics: Science and Systems, Workshop on Integrating Planning and Learning, July 2021. [Abstract] [PDF] [Cite] |
||
Abstract: We propose a method for learning constraints represented as Gaussian processes (GPs) from locally-optimal demonstrations. Our approach uses the Karush-Kuhn-Tucker (KKT) optimality conditions of the demonstrations to determine the location and shape of the constraints, and uses these to train a GP which is consistent with this information. We demonstrate our method on a 12D quadrotor constraint learning problem, showing that the learned constraint is accurate and can be used within a kinodynamic RRT to plan probabilistically-safe trajectories. |
|||
BibTeX:
@inproceedings{Wang-RSSWS-21, |
|||
 |
Learning Parametric Constraints in High Dimensions from Demonstrations Glen Chou, Dmitry Berenson, Necmiye Ozay Robotics: Science and Systems, Workshop on Robust Autonomy, June 2019. [Abstract] [PDF] [Cite] Selected for long contributed talk. |
||
Abstract: We extend the learning from demonstration paradigm by providing a method for learning unknown constraints shared across tasks, using demonstrations of the tasks, their cost functions, and knowledge of the system dynamics and control constraints. Given safe demonstrations, our method uses hit-and-run sampling to obtain lower cost, and thus unsafe, trajectories. Both safe and unsafe trajectories are used to obtain a consistent representation of the unsafe set via solving a mixed integer program. Additionally, by leveraging a known parameterization of the constraint, we modify our method to learn parametric constraints in high dimensions. We show that our method can learn a six-dimensional pose constraint for a 7-DOF robot arm. |
|||
BibTeX:
@inproceedings{Chou-RSSWS-19, |
|||
 |
Using neural networks to compute approximate and guaranteed feasible Hamilton-Jacobi-Bellman PDE solutions Frank Jiang*, Glen Chou*, Mo Chen*, Claire J. Tomlin arXiv, November 2016. [Abstract] [arXiv] [Cite] |
||
Abstract: To sidestep the curse of dimensionality when computing solutions to Hamilton-Jacobi-Bellman partial differential equations (HJB PDE), we propose an algorithm that leverages a neural network to approximate the value function. We show that our final approximation of the value function generates near optimal controls which are guaranteed to successfully drive the system to a target state. Our framework is not dependent on state space discretization, leading to a significant reduction in computation time and space complexity in comparison with dynamic programming-based approaches. Using this grid-free approach also enables us to plan over longer time horizons with relatively little additional computation overhead. Unlike many previous neural network HJB PDE approximating formulations, our approximation is strictly conservative and hence any trajectories we generate will be strictly feasible. For demonstration, we specialize our new general framework to the Dubins car model and discuss how the framework can be applied to other models with higher-dimensional state spaces. |
|||
BibTeX:
@inproceedings{Jiang-et-al-16,
author = {Frank J. Jiang and
Glen Chou and
Mo Chen and
Claire J. Tomlin},
title = {Using neural networks to compute approximate and guaranteed feasible Hamilton-Jacobi-Bellman PDE solutions},
journal = {CoRR},
volume = {abs/1611.03158},
year = {2016}, |
|||